本章介紹三個元件之間該有的原則:
- 相依要無環
- 相依要穩定
- 抽象介面要穩定
影響架構的作用力有三種:政治力、技術能力和揮發力
無環依賴原則(The Acyclic Dependencies Principle, ADP)
簡單說就是元件相依有向圖中,不得出現環
那這個原則是怎麼演化而來的呢?
很久很久以前,所有的工程師都編輯相同的一份程式碼,而他們都面臨一個「一覺醒來,發現自己在異世界」的問題。昨天下班前寫的程式明明是正常運作,怎麼早上來上班就壞了?!這是因為有人半夜連VPN,修改了同一份的程式碼,意外地,把你昨天寫的東西弄壞了。 為了解決這個夢魘,有識之士提出了 Weekly Build 週建置 星期一到星期四,人們在自己的機器上開發,避免編輯到同一份原始碼;星期五的時候,大家將各自的原始碼合併,然後建置新版的程式。因此,人們有四天可以專心開發,再也沒有「起床症候群」的困擾了。當專案很小或是人數很少的時候,大家過著幸福快樂的日子。可惜好景不常,一旦專案越來越大、人越來越多,合併原始碼所需的時間便越拉越長,單單星期五一天處理不完,於是建置時間從星期五、星期四漸漸的往週中延長。於是,時間都拿去處理合併,開發時間被壓縮自然地效率越降越低。 很顯然週建置還不足以解決問題。
消除依賴還
首先我們要把整個開發分解成一個個的小元件,而且每個元件必須是單人或一組可以負責做完的工作份量。當元件穩定的時候,開發團隊釋出負責的元件並附上版號,讓別人使用釋出的版本,同時間,開發團隊可持續開發也不會影響到使用該元件的程式碼。 如此一來,當別人釋出新的元件的時候,你可以選擇相依舊的或是新的元件,再也不會因為別人的改動讓你的程式壞掉了!我們解決了之前週建置遇到的問題:
- 別人修改的程式導致你的功能壞掉
- 不需要統一時間合併程式碼
但這個前提是相依有向圖裡面不可以有環!否則還是會發生「起床症候群」。
下圖的相依有向圖中,沒有任何的環。
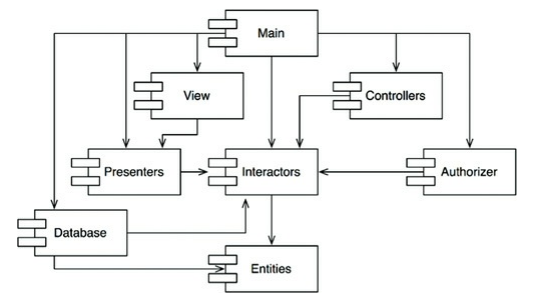
從相依有向圖,我們可以很清楚地解釋出元件的時候會對誰造成影響
- Case: Release
main在釋出新版的
main的時候,我們完全不用擔心會影響到其他的元件 - Case: Release
Presenters更新
Presenters會影響main&view,這兩個元件的開發者可以自己決定要不要跟著升級
相反的,在開發的時候只要確保相依的套件的版本是對的,就可以保證元件的功能可以正常運作。換句話說,開發者無須考慮全部的元件,只需要專注在相依的元件上即可。
當我們要釋出應用程式或是 linbrary 的時候,由底層向上層建置即可,建置程序非常的清晰明瞭。
如果有環會造成什麼影響
如果 Entities 相依於 Authorizer,使得相依有向圖變成下圖,會發生什麼事?
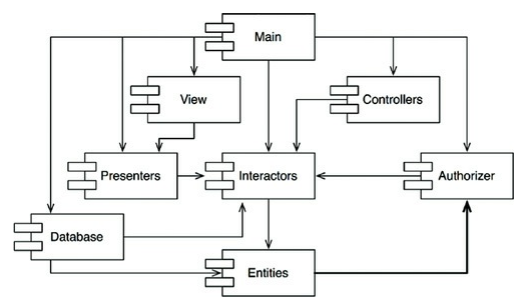
- 對於
Database來說,相依變多導致釋出Database的話,需要考慮的事情變多了 Entities,Authorizer和Interactors等效上,變成了一個新的且龐大的元件Entities,Authorizer和Interactors之中的任何修改都會相互影響- 不知道要怎麼建置
Entities
那我們要怎麼解決環的問題呢?使用 Dependency Inversion Principle (DIP)
- 在
Entities裡面新增 interfacePermission
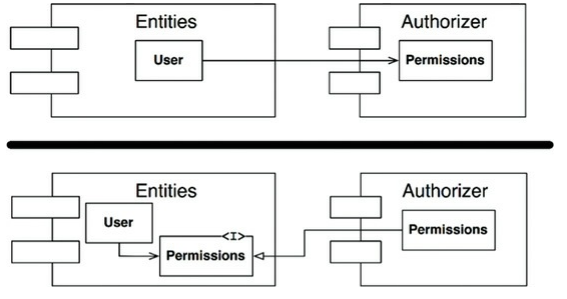
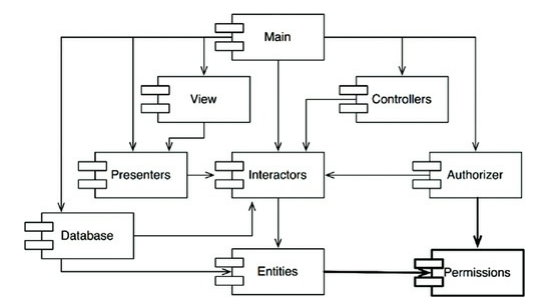
在開發過程中,我們發現元件結構經常改變,我們要時時刻刻確保有向相依圖中沒有環。
Top-Down Design
經由上面的例子,由上而下的設計模式是不存的。因為元件架構隨著開發的進程逐漸演進,不可能在開始一個專案的時候,就決定好元件的架構。隨著開發進程,我們會開始思考要如何重複利用寫好的原件,於是我們可以用 共同重復使用原則(common reuse principle, CRP) 來實作;當元件變小變多的時候,因為你不清楚別人怎麼使用你的原件,所以出現環狀相依的機率越來越大,而出現環狀相依的時候,我們會用 無環依賴原則(acyclic dependencies principle, ADP) 來解決環狀相依,而解決問題的副作用就是讓元件相依架構圖不穩定、時常改變。
另一方面,元件相依圖最重要的功能將「維護性」和「可建置性」圖像化。隨著開發我們的元件架構會越變越複雜,我們可以藉由元件相依圖來管理各個模組、元件的相依關係,以避免出現「起床症候群」,要避免「起床症候群」就要
- 各模組、元件內的修改所造成的影響範圍要本地化(越小越好)
所以在實作的時候,需要注意這兩個原則 共同封閉原則(common closure principle, CCP) 和 單一職責(single responsibility principle, SRP)。還有合併會互相影響的原件。
- 將系統內某元件經常變動的部分和不常變動的部分分開,讓常變動的元件相依不常變動元件
這樣才不會因為常變動的部分導致不變的部分壞掉
穩定依賴原則(SDP)
朝著穩定的方向進行依賴
透過符合共同封閉元則(Common Closure Principle, CCP),我們會建立對某些變化類型敏感的元件,這些元件被設計成可變的,我們預期它們會變化。 那麼對於一個預期是可變的元件,他就不應該讓另一個難以更改的元件依賴他,否則就會造原可變的元件難以更改 這就是軟體的反常的特性,就算你的模組沒有任何的修改,只要別人對你有依賴,就可以讓你的程式變得難以更改。透過遵循 單一職責(single responsibility principle, SRP) 可以確保設計成可變的模組不會被更難以更改的模組所依賴。
穩定性
- 直立的硬幣:推倒很簡單 => 穩定性低
- 桌子:推倒不簡單 => 穩定性高
使軟體元件難以變更(變穩定)的因素很多,包括規模、複雜性、清晰程度等等,但我們要來著重在另一種因素,也就是「讓其他元件依賴他」。具有許多輸入依賴關係的元件是很穩定的,因為要使所有依賴它的元件能夠相容變更,往往需要非常大的工作量
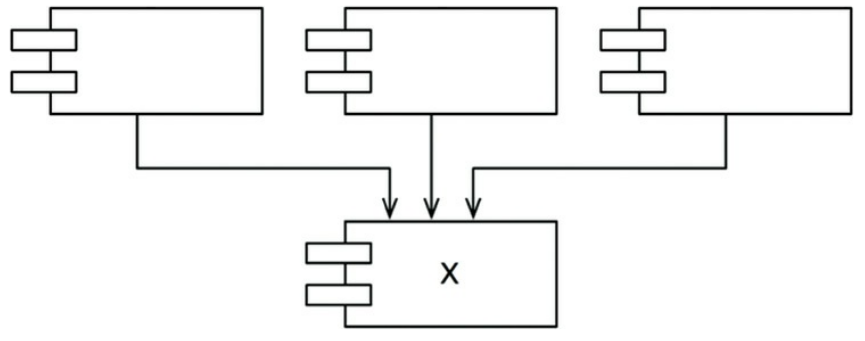
下圖是一個穩定的元件 X,有 3 個元件依賴他,因此就有 3 個理由不去更改他,相反地 X 不被任何元件依賴,所有的外部影響都不會使其改變,我們稱 X 是無依賴性的。
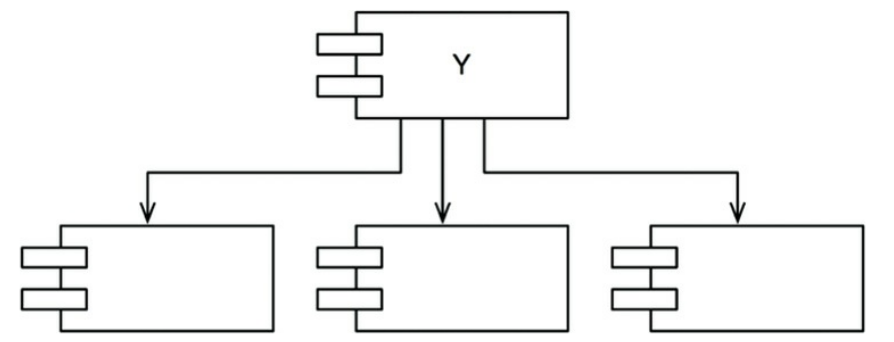
下圖是一個不穩定的元件,沒有任何元件依賴 Y,且 Y 依賴於 3 個元件,所以它具有 3 個外部更改源,我們稱 Y 是依賴性的
計算穩定性
- FadeIn:輸入依賴度 (被別人依賴)
- FadeOut:輸出依賴度 (依賴別人)
- I:不穩定性
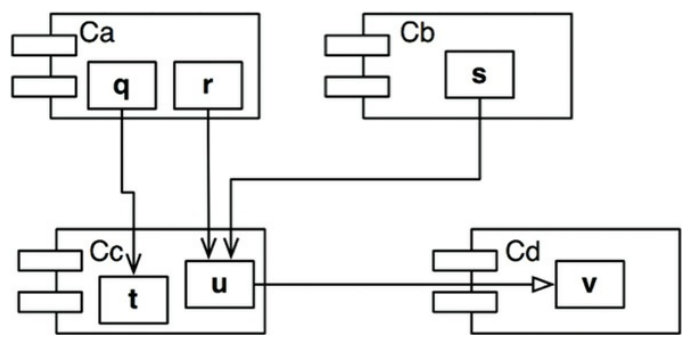
Cc 的不穩定性計算:
當 I = 1 時,代表沒有被任何元件依賴,而這個元件有依賴其他元件,這就是一個最不穩定的狀態。
當 I = 0 時,代表有被別的元件依賴但沒有依賴其他元件,它負有責任且無依賴性,處於最穩定的狀態
SDP 的規定是:一個元件的 I 值應該要大於所有他依賴的元件的 I 值 (穩定的元件不能依賴不穩定的元件)
並非所有元件都該是穩定的
下圖展示了理想的配置,把可改變的元件位於頂部並依賴於底部穩定的元件,任何向上的箭頭都意味著違反了 SDP (也會違反後面會提到的 ADP)。
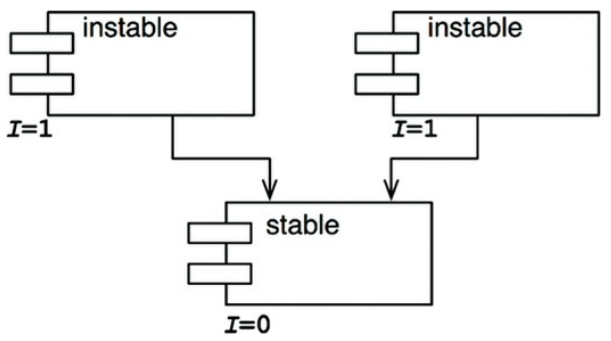
下圖展示了會違反了 SDP 的做法:
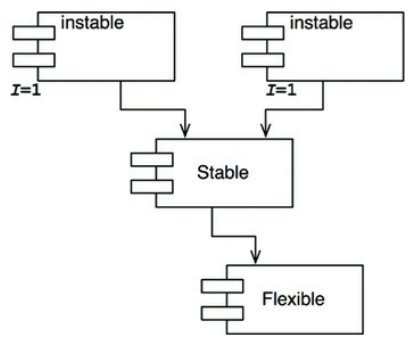
我們打算讓 Flexible 元件易於更改,我們希望他是不穩定的,如果 Stable 的元件建立了對 Flexible 的依賴,就違反了 SDP,會讓 Flexible 不再易於更改。
要解決這個問題,就必須解除依賴,假設 Flexible 中有一個 class C 被 Stable 中的 class U 依賴
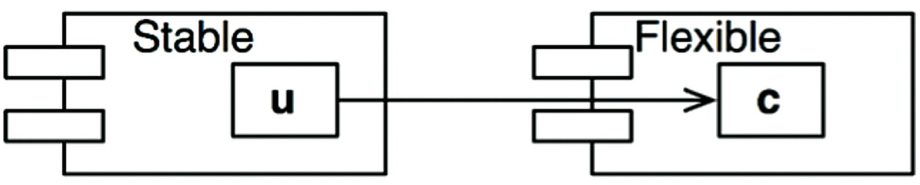
我們可以用 Dependency Inversion Principle (DIP) 來修正這個問題。
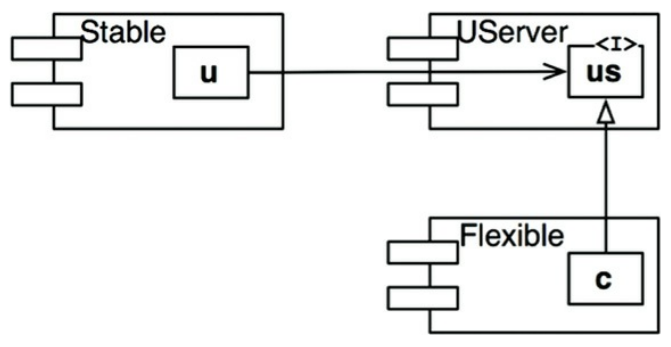
穩定抽象原則
元件的抽象程度應該與元件的穩定程度一致
高層設計的位置 (Where do we put the High-Level policy)
系統中的某些軟體不應該經常改變,我們不希望業務與架構決策是不穩定的,因此應該把「封裝系統高層設計的軟體」放入穩定的元件中 (I=0),但這就表示這些決策的程式碼會難以更變,又會使得整體架構變得不靈活
我們要怎麼讓一個高穩定性 (I=0) 的元件足夠靈活足以承受變化呢? 答案就是使用抽象類別來達成 Open-Close Principle (OCP)。
SAP 簡介
- 一個穩定的元件應該也是抽象的
- 一個不穩定的元件應該是具體的
DIP 是處理類別的原則,類別一定是抽象或是具體的,沒有灰色地帶
而 SAP 和 SDP 是針對元件的 DIP 原則,規定依賴應該朝著穩定且抽象的方向前進
計算抽象性
- Nc:元件中類別總數
- Na:元件中抽象類別及介面的總數
- A:抽象性
A = 0 就是沒有任何抽象類別,1 就是只有抽象類別
主序列 (The Main Sequence)
最穩定、最抽象的元件會位於左上角 (0,1),最不穩定、最具體的元件會位於右下角 (1,0),但並非所有元件都會落在這兩個位置,例如一個抽象類別衍生自另一個抽象類別 (抽象但不是最穩定狀態),因此我們要來找元件不應該在的位置。
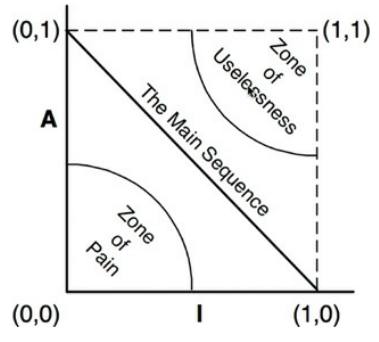
痛苦地帶
在 (0,0) 附近的元件,是一個高度穩定且具體的元件,很難擴展也很難修改
database schema 就是這樣,易變、具體、高度被依賴
工具程式庫也是,例如 String 類別,具體、高度被依賴,但不易變動
越易變的元件在 (0,0) 就越痛苦
無用地帶
在 (1,1) 附近的元件,有抽象性卻沒有被依賴,就是無用的,通常是剩下沒被用到的抽象類別,沒有被人實作。
主序列
為了遠離無用地帶跟痛苦地帶 我們希望我們的元件可以分佈在(0,1)到(1,0)的線上 作者稱為主序列(Main Sequence) 既然我們知道越靠近主序列越好 那麼對於評價一個元件而言 我們就可以計算這個元件到主序列的距離

當我們量化了一個元件的好壞以後 我們就可以盡情地分析我們的系統啦
你可以用任何你會的統計知識 mean(平均數) variance(變異數) SD(標準差)等等 把一個系統內的所有元件的座標畫在座標圖上
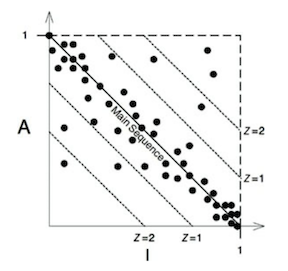
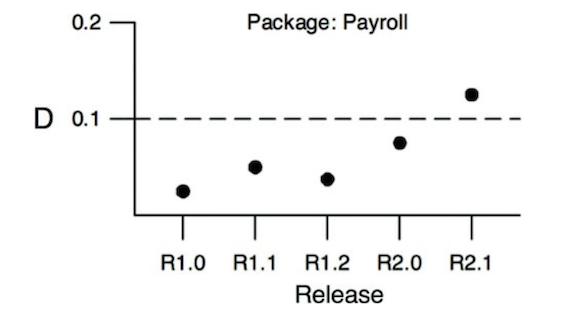
如上圖,我們可以針對超過一個標準差(Z>1)的元件做檢查
另一種是對某個元件依時間畫出 D 值的變化,並設定一個 threshold,並檢查超過 threshold 的元件